UNIVERZITET U BEOGRADU GRA EVINSKI FAKULTET
|
|
|
- Janis Kaņeps
- pirms 1 gadiem
- Skatījumi:
Transkripts
1 UNIVERZITET U BEOGRADU GRA EVINSKI FAKULTET www@grf.bg.c.rs Studijski progrmi: GRA EVINARSTVO OSNOVNE AKADEMSKE STUDIJE 22 Godin/Semestr: PRVA GODINA/DRUGI SEMESTAR Nziv predmet (ifr): MATEMATIKA 2 (B3O2M2) Nstvnik: ALEKSANDRA ERI Nslov predv : ODRE ENI Beogrd, 222. Sv utorsk prv utor prezentcije i/ili video snimk su ztien. Snimk ili prezentcij se mogu koristiti smo z nstvu n d inu student Grevinskog fkultet Univerzitet u Beogrdu u kolskoj 22/222 i ne mogu se koristiti z druge svrhe bez pismene sglsnosti utor mterijl.
2 Odreeni integrli Z konqn skup tqk π = {,, 2..., n, n }, z koje vi = < < 2 < < n < n = b, kemo d je jedn podel segment [, b] R. D e, s i, z i [n], emo oznqvti rzliku i := i i. Mksimlnu vrednost skup {, 2, 3,..., n } nzivmo i prmetrom podele π i oznqvmo s λ(π) := m i [n] i. D e, uoqimo skup tqk ξ = {ξ, ξ 2,..., ξ n }, tkvih d ξ i [ i, i ] z svko i [n]. Td z ureeni pr (π, ξ) kemo d je jedn podel segment [, b] s istknutim tqkm. f(ξ n) = f() f(ξ 3) f(ξ 2) f(ξ ) ξ ξ2 2 ξ3 3 n n ξn Definicij Nek je f : [, b] R jedn funkcij i (π, ξ) nek podel segment [, b] s istknutim tqkm. Z zbir σ(f, π, ξ) := f(ξ i ) i kemo d je integrlni zbir funkcije f z dtu podelu (π, ξ).
3 Primer Posmtrjmo funkciju f() = c koj je definisn z [, b]. I nek je π = {,, 2,..., n } proizvo n podel segment [, b] i ξ = {ξ, ξ 2,..., ξ n } skup istknutih tqk podele P. Kko z svko i [n] vi f(ξ i ) = c, jsno je d integrlni zbir iznosi σ(f, π, ξ) = f( i ) i = c i = c i = c(b ). Definicij 2 Broj I je odreeni integrl funkcije f n segmentu [, b] ko i smo ko je Drugim reqim, ko i smo ko lim σ(f, π, τ) = I. λ(π) ( ε > )( δ > )( (π, ξ) P[, b])(λ(π) < δ = I σ(f, π, ξ) < ε), gde je P[, b] skup svih podel segment [, b]. Odreeni integrl I funkcije f n segmentu [, b] emo oznqvti s f() d. I jo, z funkciju f emo rei d je integrnd (podintegrln funkcij), z brojeve i b d su do i gro grnic odreenog integrl. Ukoliko postoji odreeni integrl funkcije f n segmentu [, b], kzemo d je f integrbiln (po Rimnu) n [, b] i pisti f R[, b], gde je s R[, b] oznqen skup svih integrbilnih funkcij n segmentu [, b]. Primer 2 U prethodnom primeru smo pokzli d z konstntnu funkciju f i proizvo nu podelu s istknutim tqkm (π, ξ) vi σ(f, π, ξ) = c(b ), odkle zk uqujemo d je c d = Specijlno, ko je c = dobijmo lim σ(f, π, ξ) = c(b ). λ(π) d = b. Stv (Potrebn uslov) Potrebn uslov d f() bude integrbiln n segmentu [, b] jeste d funkcij bude ogrniqen n emu. Obrnuto ne vi. To jest, ukoliko je funkcij f() ogrniqen n nekom intervlu [, b], td ne moemo zk uqiti d je funkcij i integrbiln n istom intervlu.
4 Primer 3 Posmtrjmo Dirihleovu funkciju χ koj je definisn s {, [, b] i je rcionln broj, χ() =, [, b] i je ircionln broj. Posmtrjmo bilo koju podelu π P[, b] i dv izbor tqk ξ, ξ, li tko d su sve tqke ξ i ξ iz prvog izbor rcionlne, sve tqke ξ j ξ ircionlne. Td ve sledee jednkosti σ(χ, π, ξ ) = i = b i σ(χ, π, ξ ) = i =, i= odkkle zk uqujemo d grniqn vrednost lim λ(π) σ(χ, π, ξ) ne postoji. Teorem Ve slede tvre :. Ukoliko je f neprekidn n [, b], ond je f integrbiln n [, b]. 2. Ukoliko je f monoton n [, b], ond je f integrbiln n [, b]. Osobine odreenog integrl Stv 2 Ukoliko f R[, b], td vi slede jednkost f() d = b f() d. Dokz. Nek je π = {,,..., n } proizvo n podel intervl [, b], td vi slede jednkost f(ξ i )( i i ) = f(ξ i )( i i ), Jsno je d kd λ(π) dobijmo d je f() d = f() d. b Posledic Ukoliko je funckij f definisn u tqki, td vi f() d =.
5 Stv 3 (Aditivnost odreenog integrl) Ako z relne brojeve, b i c vi < b < c i ukoliko je funkcij f integrbiln n segmentu [, c], ond je integrbiln i n segmentim [, b] i [b, c] i jo vi c f() d = f() d + c b f() d. Stv 4 (Linernost odreenog integrl) Nek su f, g R[, b] i α, β R. Td je αf + βg R[, b] i jo vi: (αf() + βg()) d = α f() d + β g() d. Dokz. Z integrlne sume proizvo ne podele π vi slede jednkost σ(αf + βg, π, ξ) = (αf(ξ i ) + βg(ξ i )) i = α f(ξ i ) i + β g(ξ i ) i = ασ(f, π, ξ) + βσ(g, π, ξ). Prem pretpostvci f i g su integrbilne n [, b], p postoje grniqne vrednosti lim λ(π) σ(f, π, ξ) i lim λ(π) σ(g, π, ξ) i vi lim σ(αf + βg, π, ξ) = α lim σ(f, π, ξ) + β lim σ(g, π, ξ), λ(π) λ(π) λ(π) to je i treblo pokzti. Stv 5 (Monotonost odreenog integrl) Nek su f, g R[, b] i nek z svko [, b] vi f() g(). Td vi slede nejednkost: f() d g() d. Dokz. Z integrlne sume proizvo ne podele π vi slede nejednkost σ(f, π, ξ) = f(ξ i ) i g(ξ i ) i = σ(g, π, ξ). Prem pretpostvci f i g su integrbilne n [, b], p postoje grniqne vrednosti lim λ(π) σ(f, π, ξ) i lim λ(π) σ(g, π, ξ) i vi to je i treblo pokzti. lim σ(f, π, ξ) λ(π) lim σ(g, π, ξ), λ(π)
6 Posledic 2 Nek je f R[, b] i nek z svko [, b] vi f(). Td vi slede nejednkost: f() d. Teorem 2 (Teorem o sred oj vrednosti integrlnog rqun) Nek je f R[, b] i nek je m = inf f() i M = sup f(). [,b] [,b] Td postoji µ [m, M] tko d vi f() d = µ(b ). Ukoliko je jo i f neprekidn n segemntu [, b], td postoji c [, b] tko d vi f() d = f(c)(b ). Dokz. Kko z svko [, b] vi m f() M, to tqno znqi d je z svku podelu π tqn i slede nejednkost m(b ) = m i f(ξ i ) i M i = M(b ). Jsno je d td vi m(b ) f()d M(b ). Ako je = b, tren jednkost je trivijlno ispu en. Ukoliko je b vi b m f()d M, (b ) odkle proizilzi d postoji broj µ [m, M] koji zdovo v trenu jednkost. Ukoliko je f neprekidn n segmentu [, b], on dostie svoju njm u m = f(α) i njveu M = f(β) vrednost, z neke α, β [, b]. Prem Bolcno - Koijevoj teoremi o meuvrednosti postoji c [, b] tko d je µ = f(c), qime je teorem dokzn.
7 Ukoliko je f R[, b] i f(), z svko [, b], ond odreeni integrl f() d odgovr povrini povri ogrniqene krivom = f() i b prvm =, = b i =. D e, teorem o sred oj vrednosti integrlnog rqun nm ke d pomenut povrin odgovr i povrini prvougonik s strnicm b i µ. = f() = f() P µ P b c b Vez izmeu odreenog integrl i izvod Definicij 3 Nek je f R[, b]. Funkciju φ definisnu s φ() := f(t) dt z [, b], nzivmo integrlom s promen ivom gor om grnicom. Stv 6 Ako je f R[, b], ond φ C[, b]. Dokz. Koristei teoremu o sred oj vrednosti integrlnog rqun, z tqke, [, b] vi slede jednkost φ() φ( ) = f(t) dt f(t) dt = f(t) dt + f(t) dt f(t) dt = f(t) dt = µ( ). Jsno je d vi slede jednkost lim φ() = φ( ), p zk uqujemo d je f neprekidn funkcij u tqki.
8 Stv 7 Ako je f C[, b], td je φ primitivn funkcij funkcije f n segmentu [, b], to jest z sve [, b] vi φ () = f(). Dokz. Nek je h > tko d + h [, b], td koristei teoremu o sred oj vrednosti z neprekidnu funkciju f nlzimo d je φ( + h) φ( ) = ( +h ) f(t) dt f(t) dt = +h f(t) dt h h h = h f(c) ( + h ) = f(c), z neko c [, + h]. To tqno znqi d postoji k [, ] tko d je c = + kh. Ukoliko h, ond c, p iz neprekidnosti funkcije f dobijmo d f(c) f( ). Jsno je d vi slede jednkost φ ( ) = lim h φ( + h) φ( ) h to je i treblo pokzti. = lim h f( + kh) = f( ), Teorem 3 ( utn - Ljbnicov formul) Nek je f C[, b] i nek je F bilo koj primitivn funkcij funkcije f n [, b]. Td vi f() d = F () b = F (b) F (). Dokz. N osnovu prethodnog stv, funkcij φ() = f(t) dt je primitivn funkcij funkcije f n [, b], p se funkcije F i φ rzlikuju smo do n konstntu. Drugim reqim, postoji C R tko d z svko [, b] vi φ() = F () + C. Primetimo d, z =, dobijmo jednkost = f(t) dt = φ() = F () + C, odkle sledi d je C = F (). D e, z = b dobijmo d je to je i treblo pokzti. f(t) dt = φ(b) = F (b) + C = F (b) F (),
9 Primer 4 Primer 5 Utvrdimo d ve sledee jednkosti e d = e = e i π/2 cos d = sin π/2 =. Posmtrjmo funkciju 2, koj je z [ 2, 2] odreen s { 2 2, [ 2, ] [, 2], = 2, (, ). f() Utvrdimo d vi slede jednkost 2 Primer d = 2 ( 2 ) d + ( ) 2 = ( 2 3 ( 2 ) d + ) 2 ( 2 ) d ( ) = 4. Posmtrjmo funkciju sgn( 2 ), koj je z [ 2, 2] odreen s +, [ 2, ) (, 2], sgn( 2 ) =, {, },, (, ). f() Utvrdimo d vi slede jednkost 2 2 sgn( 2 ) d = 2 d 2 d + d = =.
10 Smen promen ive Stv 8 Nek je f C[, b], funkcij ϕ : [α, β] [, b] im neprekidn izvod i vi ϕ(α) = i ϕ(β) = b. Td vi jednkost f() d = β α f(ϕ(t))ϕ (t) dt. Stv 9 Nek je f R[, b], strogo monoton funkcij ϕ : [α, β] [, b] im neprekidn izvod i vi ϕ(α) = i ϕ(β) = b. Td vi jednkost f() d = β α f(ϕ(t))ϕ (t) dt. Posledic 3 Nek je f C[, ]. Ve slede tvre :. Ako je funkcij f prn, td je f() d = 2 2. Ako je funkcij f neprn, td je f() d =. f() d. Dokz. Koristei smenu t =, dt = d, dobijmo sledeu jednkost: f() d = = f() d + f( t) dt + f() d = f( t) dt + f() d.. Ako je funkcij f prn, td vi f( t) = f(t), p je f() d = f(t) dt + f() d = 2 f() d. 2. Ako je funkcij f neprn, td vi f( t) = f(t), p je f() d f() d = f(t) dt + f() d =.
11 Primer 7 Primetimo d z funkciju f() = 3 vi f( ) = ( ) 3 = 3 = f(), odkle zk uqujemo d je f() neprn funkcij. N osnovu prethodne posledice zk uqujemo d je Z funkciju g() = + 2 vi g( ) = 3 d =. + ( ) 2 = + 2 = g(), odkle zk uqujemo d je g() prn funkcij. N osnovu prethodne posledice zk uqujemo d je d + 2 = 2 d + 2 = 2 rctg = 2 rctg 2 rctg = π 2. Primer 8 Primetimo d vi slede jednkost 3π/4 π/4 sin d = π/4 π/4 sin d + 3π/4 π/4 sin d. Poto je funkcij sin neprn, zk uqujemo d je prvi integrl jednk nuli, p vi 3π/4 3π/4 3π/4 sin d = sin d = ( cos ) π/4 π/4 π/4 e d Zdtk Izrqunti (ln 2 + ). = cos 3π ( 4 cos π ) = 2. 4 Ree e. Koristei smenu t = ln, dt = d/, dobijmo sledeu jednkost e d (ln 2 + ) = Zdtk 2 Izrqunti dt t 2 + = rctg t cos rctg d ln( + 2. ) = rctg rctg = π 4. Ree e. Primetimo d je podintegrln funkcij f() neprn, to jest vi f( ) = cos( ) rctg( ) ln( + ( ) 2 ) cos rctg = ln( + 2 = f(), ) p zk uqujemo d je treni integrl jednk nuli.
12 Prcijln integrcij Stv Nek funkcije u() i v() imju neprekidne izvode n segmentu [, b]. Td vi slede jednkost Primer 9 jednkost e u()v ()d = u()v() b u ()v()d. Uvodei u = ln, du = d/ i dv = d, v = 2 2, dobijmo sledeu ln d = 2 2 ln Zdtk 3 Izrqunti I = e π e 2 2 d = 2 ln ( sin ) 2 d i I 2 = Ree e. Primetimo d vi slede jednkost π I + I 2 = 2 d = 3 π 3 S druge strne, immo d je π I 2 I = 2 cos 2 d = 2 sin 2 π 2 cos 2 π = 2 π cos 2 d = π 2 2 Jsno je d vi I = π 2 ( π ) i I 2 = π 2 e π = π3 3. π 2 4 e ( cos ) 2 d. = e sin 2 d sin 2 π 4 = π 2. ( π ). Primen odreenog integrl Duin luk krive Jedn od glvnih primen integrlnog rqun jeste rqun e duine luk krive l. Nime, ko je kriv eksplicitno odreen s = f(), gde je f neprekidno diferencijbiln funkcij n intervlu [, b], ond je duin luk krive jednk l = + f 2 () d.
13 Posmtrjmo neprekidno diferencijbilnu funkciju f : [, b] R i neku podelu π = {,, 2,..., n, n } segment [, b]. Td duin poligonijlne linije A, A, A 2,..., A n, A n, gde je A i ( i, f( i )) z i n, iznosi l n = (i i ) 2 + (f( i ) f( i ) 2. Prem Lngrnovoj teoremi, z svko i [n], postoji tqk ξ i [ i, i ] tko d vi f( i ) f( i ) = f (ξ i )( i i ), odkle proizilzi d je duin poligonijlne linije jednk l n = (i i ) 2 + (f (ξ i )) 2 ( i i ) 2 = + (f (ξ i )) 2 ( i i ). Primetimo d je l n integrlni zbir funkcije + (f ()) n segmentu [, b], to jest vi slede jednkost ( ) l n = σ + (f ) 2, π, ξ = + (f (ξ i )) 2 i. Prem tome, jsno je d je duin luk krive iznosi l = Primer gor eg polukrug ( ) lim l n = lim σ + (f ) 2, π, ξ = λ(π) λ(π) + (f ()) 2 d. Posmtrjmo krug qij jednqin glsi = r 2. Td je jednqin f() = r 2 2. Duin poluobim posmtrnog krug iznosi r r ( ) + f 2 2 r r () d = + d = r r r 2 2 r r 2 d = r rcsin r 2 r, r odkle zk uqujemo d je obim posmtrnog krug jednk 2rπ.
14 = = b (, ) (b, ) (b, f(b)) (, f()) = f() (, f()) (, ) (b, f(b)) (b, ) = = f() = b Povrin del rvni Posmtrjmo f C[, b] tkvu d je f() z svko [, b]. Povrin krivolinijskog trpez ogrniqenog krivom = f() i prvm =, = b i = odgovr odreenom integrlu P = f() d. Ukoliko je funkcij f n intervlu [, b] negtivn, vrednost integrl f() d bie negtivn, li N osnovu prethodnog rzmtr sledi d je povrin krivolonijkog e po psolutnoj vrednosti odgovrti povrini krivolinijskog trpez. trpez ogrniqnenog krivom = f() i prvm =, = b i = jednk P = f() d. Nek su funckije f i g neprekidne n intervlu [, b] i nek je f() g(), z sve [, b]. Povrin del rvni ogrniqenog krivm = f() i = g() i prvm = i = b je jednk P = (f() g()) d. (, f()) (, g()) (, ) = = g() = f() = b (b, f(b)) (b, g(b)) (b, )
15 Zdtk 4 Odrediti povrinu onog del rvni koji je ogrniqen krivom = i prvom + = 3. Ree e. Posmtrjmo deo rvni koji je ogrniqen dtim krivm. Nije teko utvrditi d se posmtrne krive seku u tqkm (, 3) i (3, ). Uz to je gro grnic odreen funkcijom = , dok je do odreen s = 3. Prem tome, tren povrin je jednk (, 3) = P = 3 (( ) (3 )) d, + = 3 odkle dobijmo d je P = 3 ( 2 +3) d = ) ( = (3, ) Zdtk 5 Odrediti povrinu onog del rvni koji je ogrniqen krivom = / 2 i prvm = i = 4. Ree e. Posmtrjmo deo rvni koji je ogrniqen dtim krivm. Utvrdimo d se krive:. = / 2 i = 4 seku u tqki (/2, 4), 2. = / 2 i = seku u tqki (, ), 3. = 4 i = seku u tqki (4, 4). ( 2, 4) = 4 (4, 4) P P 2 = Kko do grnic nije jedinstveno odreen, neophodno je d trenu povrinu del rvni P podelimo n dv del P i P 2, gde su P = (4 ) 4 2 d i P 2 = (4 ) d. /2 (3, ) = / 2 Dkle, tren povrin iznosi P = P + P 2 = ( 4 + ) + /2 ) (4 2 4 = 2 2.
16 Zdtk 6 Odrediti povrinu del rvni koj je ogrniqen krivm = + 3 i = 3. Ree e. Primetimo d ve sledee jednkosti: { + + 3, 3, + 3 = i 3 = 3, < 3, { +3,, 3, <. (2, 5) = + 3 = 3 (, 3) = 3 = 3 (, 2) P P 2 ( 3, ) (, ) Utvrdimo jo d se prve + 3 i 3 seku u tqki (2, 5), prve + 3 i 3 u tqki ( 3, ). Poto do grnic nije jedinstveno odreen, neophodno je d trenu povrinu del rvni P podelimo n dv del P i P 2, gde su P = (( + 3) ( 3 )) d i P 2 = Konqno, tren povrin iznosi P = P + P 2 = (4 + 4) d ( 2 + 4) d = ( ) (( + 3) (3 )) d. + ( 2 + 4) Npomen. Primetimo d P odgovr povrini trougl qij je duin strnice 4 visin, dok P 2 odgovr povrini trougl qij je strnic 4 visin 2. Zdtk 7 Odrediti povrinu onog del rvni koji je ogrniqen krivom ln( 2) i prvm = e, = e 2 i =. Ree e. Posmtrjmo grfike zdtih krivi i utvrdimo d je tren povrin P jednk P = P + P 2, gde su P = 3 e ( ln( 2)) d i P 2 = e 2 3 (ln( 2) ) d. 2 = 6.
17 = e = e 2 = ln( 2) (e 2, ln(e 2 2)) P P 2 (e, ) (e, ln(e 2)) (3, ) Koristei smenu t = 2, dt = d, dobijmo 3 e 2 P = ln( 2) d + ln( 2) d = ln t dt + e 3 e 2 = (e 2) ln(e 2) + (e 2 2) ln(e 2 2) + 6 e e 2. e 2 2 ln t dt Zdtk 8 Odrediti povrinu onog del rvni koji je ogrniqen krivom = i prvm 2 =, = 2 i =. Ree e. Utvrdimo d je tren povrin jednk P = P + P 2, gde su povrine P i P 2 odreene s 2 ( ( P = ( 2 ) d i P 2 = 2 )) d. 2 = 2 = / (, ) = 2 2 (, ) P P 2 (, ) (2, /2) Jsno je d vi slede jednkost P = P + P 2 = (ln 2 4 ) 2 = ln(2).
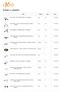
Nr. p.k.* Transporta līdzekļa marka / modelis Transporta līdzekļa veids Valsts Reģ. Nr. saraksts un sākuma cenas izsolei Stopiņu novada Lī
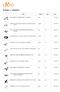
 1 FIAT DOBLO Kravas transporta HA8036 2008 1368 Benzīns 95 159 724 2 (slikts) 1 000.00 826.45 TEC-2, Acone, 2 FIAT DOBLO Kravas transporta HA8085 2008 1368 Benzīns 95 167 599 3 (viduvējs) 1 700.00 1404.96
1 FIAT DOBLO Kravas transporta HA8036 2008 1368 Benzīns 95 159 724 2 (slikts) 1 000.00 826.45 TEC-2, Acone, 2 FIAT DOBLO Kravas transporta HA8085 2008 1368 Benzīns 95 167 599 3 (viduvējs) 1 700.00 1404.96
Latvijas Universitāte Fizikas un matemātikas fakultāte Matemātiskās analīzes katedra Inese Bula HAOSS LEKCIJU KONSPEKTS 2008
 Latvijas Universitāte Fizikas un matemātikas fakultāte Matemātiskās analīzes katedra Inese Bula HAOSS LEKCIJU KONSPEKTS 2008 SATURS Kursa prasības 3 Nodaļa Nr.1: Pamatjēdzieni 4 Nodaļa Nr.2: Reālu skaitļu
Latvijas Universitāte Fizikas un matemātikas fakultāte Matemātiskās analīzes katedra Inese Bula HAOSS LEKCIJU KONSPEKTS 2008 SATURS Kursa prasības 3 Nodaļa Nr.1: Pamatjēdzieni 4 Nodaļa Nr.2: Reālu skaitļu
A/S"Fēnikss""(reģ.nr.: ) Apstiprinu: Pumpuru vidusskolas direktore Irēna Kausiniece Pumpuru vidusskola 2019.gada Dienas ēdienkarte pirmsskol
 Pumpuru vidusskol 2019.gd s ēdienkrte pirmsskols izglītojmjiem (5-6g) 5dienām Dtu ms Lik posmā: 27.05.19.-31.05.19. Tuki Ogļhidr āti 27.05. Rīsu pārslu biezputr r ievārījumu PK 150/10 189,2 6,2 2,3 24
Pumpuru vidusskol 2019.gd s ēdienkrte pirmsskols izglītojmjiem (5-6g) 5dienām Dtu ms Lik posmā: 27.05.19.-31.05.19. Tuki Ogļhidr āti 27.05. Rīsu pārslu biezputr r ievārījumu PK 150/10 189,2 6,2 2,3 24
Krājumā saīsinātā pierakstā sniegti pamatskolas ģeometrijas kursā sastopamie galvenie ģeometriskie jēdzieni, figūru īpašības, teorēmu formulējumi un a
 Krājumā saīsinātā pierakstā sniegti pamatskolas ģeometrijas kursā sastopamie galvenie ģeometriskie jēdzieni, figūru īpašības, teorēmu formulējumi un aprēķinu formulas, kas nepieciešamas, risinot uzdevumus.
Krājumā saīsinātā pierakstā sniegti pamatskolas ģeometrijas kursā sastopamie galvenie ģeometriskie jēdzieni, figūru īpašības, teorēmu formulējumi un aprēķinu formulas, kas nepieciešamas, risinot uzdevumus.
8.TEMATS RIŅĶI UN DAUDZSTŪRI Temata apraksts Skolēnam sasniedzamo rezultātu ceļvedis Uzdevumu piemēri M_10_SP_08_P1 Ar riņķa līniju saistītie leņķi Sk
 8.TEMTS RIŅĶI UN DUDZSTŪRI Temata apraksts Skolēnam sasniedzamo rezultātu ceļvedis Uzdevumu piemēri M_10_SP_08_P1 r riņķa līniju saistītie leņķi Skolēna darba lapa M_10_UP_08_P1 pvilkts daudzstūris Skolēna
8.TEMTS RIŅĶI UN DUDZSTŪRI Temata apraksts Skolēnam sasniedzamo rezultātu ceļvedis Uzdevumu piemēri M_10_SP_08_P1 r riņķa līniju saistītie leņķi Skolēna darba lapa M_10_UP_08_P1 pvilkts daudzstūris Skolēna
32repol_uzd
 Materiāls ņemts no grāmatas: Andžāns Agnis, Bērziņa Anna, Bērziņš Aivars "Latvijas Republikas 6-5 matemātikas olimpiādes" LATVIJAS REPUBLIKAS OLIMPIĀDE UZDEVUMI 8 klase Pierādīt, ka neviens no skaitļiem
Materiāls ņemts no grāmatas: Andžāns Agnis, Bērziņa Anna, Bērziņš Aivars "Latvijas Republikas 6-5 matemātikas olimpiādes" LATVIJAS REPUBLIKAS OLIMPIĀDE UZDEVUMI 8 klase Pierādīt, ka neviens no skaitļiem
Saturs Sākums Beigas Atpakaļ Aizvērt Pilns ekrāns 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studij
 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Lineārā algebra II 4.lekcija Docētājs: Dr. P. Daugulis 2012./2013.studiju
1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Lineārā algebra II 4.lekcija Docētājs: Dr. P. Daugulis 2012./2013.studiju
Saturs Sākums Beigas Atpakaļ Aizvērt Pilns ekrāns 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studij
 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Polinomu algebra 2.lekcija Docētājs: Dr. P. Daugulis 2012./2013.studiju
1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Polinomu algebra 2.lekcija Docētājs: Dr. P. Daugulis 2012./2013.studiju
Ekstrēmu uzdevumu risināšanas metodes
 LU A. Lieps Neklātienes mtemātiks skol A. Vsiļevsk, L. Rmān, A. Andžāns EKSTRĒMU UZDEVUMU RISINĀŠANAS METODES Rīg, 997 Sturs Ievds.... Kvdrātfunkcij... Uzdevumi.... Skrī strp divu skitļu vidējo ritmētisko
LU A. Lieps Neklātienes mtemātiks skol A. Vsiļevsk, L. Rmān, A. Andžāns EKSTRĒMU UZDEVUMU RISINĀŠANAS METODES Rīg, 997 Sturs Ievds.... Kvdrātfunkcij... Uzdevumi.... Skrī strp divu skitļu vidējo ritmētisko
PowerPoint Presentation
 Rīgas Tehniskās universitātes Ģeomātikas katedra LU 77. SZK sekcija «Ģeodinamika un ģeokosmiskie pētījumi 2019» Jānis Kaminskis, Mārtiņš Reiniks, Anete Kiopa 22.03.2019. 1 Atrašanās vieta 2 56 56'39.3"N
Rīgas Tehniskās universitātes Ģeomātikas katedra LU 77. SZK sekcija «Ģeodinamika un ģeokosmiskie pētījumi 2019» Jānis Kaminskis, Mārtiņš Reiniks, Anete Kiopa 22.03.2019. 1 Atrašanās vieta 2 56 56'39.3"N
A9R1q9nsan_v63m4l_2ow.tmp
 Studiju programmas raksturojums 2015./2016. a 1. uzdevumi. Programm Studiju programmas. 1. Sagatavot. 2. N. 3. N 1 2. 4. V. 5., balstoties noteikt izm Studiju programmas uzdevumi. 1.. 2. V ir. 3. Nodro.
Studiju programmas raksturojums 2015./2016. a 1. uzdevumi. Programm Studiju programmas. 1. Sagatavot. 2. N. 3. N 1 2. 4. V. 5., balstoties noteikt izm Studiju programmas uzdevumi. 1.. 2. V ir. 3. Nodro.
Microsoft Word - du_4_2005.doc
 @ 2004 Pēteris Dugulis 1 KOPU APJOMS Kā slīdzināt kops vi skitīt elementus kopās? Dbisks kopu slīdzināšns veids ir ttēlot vienu kopu otrā jeb konstruēt unkcijs no viens kops uz otru. DEFINĪCIJA Divs kops
@ 2004 Pēteris Dugulis 1 KOPU APJOMS Kā slīdzināt kops vi skitīt elementus kopās? Dbisks kopu slīdzināšns veids ir ttēlot vienu kopu otrā jeb konstruēt unkcijs no viens kops uz otru. DEFINĪCIJA Divs kops
Environment. Technology. Resorces 1999 LITERATŪRA 1. Bankovskis P. Ekoloģijas makdonalds vai bruņinieku ordenis //Diena - SestDiena. i aug. 2.
 LITERATŪRA 1. Bankovskis P. Ekoloģijas makdonalds vai bruņinieku ordenis //Diena - SestDiena. i 995. 12.aug. 2. Bērziņa I. Ceļā uz ekoloģisko kultūru //Vide. Nr.2. - 1991. 3. Bojārs J. Starptautiskās tiesības.
LITERATŪRA 1. Bankovskis P. Ekoloģijas makdonalds vai bruņinieku ordenis //Diena - SestDiena. i 995. 12.aug. 2. Bērziņa I. Ceļā uz ekoloģisko kultūru //Vide. Nr.2. - 1991. 3. Bojārs J. Starptautiskās tiesības.
Saturs Sākums Beigas Atpakaļ Aizvērt Pilns ekrāns 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studij
 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Polinomu algebra 3.lekcija Docētājs: Dr. P. Daugulis 2007./2008.studiju
1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Polinomu algebra 3.lekcija Docētājs: Dr. P. Daugulis 2007./2008.studiju
Saturs Sākums Beigas Atpakaļ Aizvērt Pilns ekrāns 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studij
 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Lineārā algebra I 5.lekcija Docētājs: Dr. P. Daugulis 2012./2013.studiju
1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Lineārā algebra I 5.lekcija Docētājs: Dr. P. Daugulis 2012./2013.studiju
tblVisiNrPos1
 Tautas skrējiens Mārupe 2008 Jaunārupe, 13.09.2008 Individuālie rezultāti Galvenais tiesnesis: Galvenais sekretārs: Māris Ozoliņš SE, distance 4000 1. 69 Vanesa Belova 1999 LSC 0:25:03 9,58 2. 67 Aleksa
Tautas skrējiens Mārupe 2008 Jaunārupe, 13.09.2008 Individuālie rezultāti Galvenais tiesnesis: Galvenais sekretārs: Māris Ozoliņš SE, distance 4000 1. 69 Vanesa Belova 1999 LSC 0:25:03 9,58 2. 67 Aleksa
DAUGAVPILS UNIVERSITĀTE MATEMĀTISKĀS ANALĪZES KATEDRA Armands Gricāns Vjačeslavs Starcevs Lebega mērs un integrālis (individuālie uzdevumi) 2002
 DAUGAVPILS UNIVERSITĀTE MATEMĀTISKĀS ANALĪZES KATEDRA Armands Gricāns Vjačeslavs Starcevs Lebega mērs un integrālis (individuālie uzdevumi) 2002 . variants skaitļiem, kuri var tikt izteikti 5 skaitīšanas
DAUGAVPILS UNIVERSITĀTE MATEMĀTISKĀS ANALĪZES KATEDRA Armands Gricāns Vjačeslavs Starcevs Lebega mērs un integrālis (individuālie uzdevumi) 2002 . variants skaitļiem, kuri var tikt izteikti 5 skaitīšanas
Nevienādības starp vidējiem
 Nevienādības starp vidējiem Mārtin, š Kokainis Latvijas Universitāte, NMS Rīga, 07 Ievads Atrisināt nevienādību nozīmē atrast visus tās atrisinājumus un pierādīt, ka citu atrisinājumu nav. Pierādīt nevienādību
Nevienādības starp vidējiem Mārtin, š Kokainis Latvijas Universitāte, NMS Rīga, 07 Ievads Atrisināt nevienādību nozīmē atrast visus tās atrisinājumus un pierādīt, ka citu atrisinājumu nav. Pierādīt nevienādību
Saturs Sākums Beigas Atpakaļ Aizvērt Pilns ekrāns 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Maǧistra studiju
 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Maǧistra studiju programma Matemātika Studiju kurss Diskrētā matemātika 5.lekcija Docētājs: Dr. P. Daugulis 2012./2013.studiju
1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Maǧistra studiju programma Matemātika Studiju kurss Diskrētā matemātika 5.lekcija Docētājs: Dr. P. Daugulis 2012./2013.studiju
Kurzemes plānošanas reģiona īstenotie pasākumi vienotā DI komunikācijas stratēģijas ietvaros gadā
 www.kurzemevisiem.lv Projekta Kurzeme visiem ieviešanas aktualitātes Kurzemes plānošanas reģions Talsos, 27.03.2019 Par projektu Kurzeme visiem Projekta «Kurzeme visiem» mērķis palielināt Kurzemes reģionā
www.kurzemevisiem.lv Projekta Kurzeme visiem ieviešanas aktualitātes Kurzemes plānošanas reģions Talsos, 27.03.2019 Par projektu Kurzeme visiem Projekta «Kurzeme visiem» mērķis palielināt Kurzemes reģionā
Saturs Sākums Beigas Atpakaļ Aizvērt Pilns ekrāns 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studij
 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Polinomu algebra 11.lekcija Docētājs: Dr. P. Daugulis 2008./2009.studiju
1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Polinomu algebra 11.lekcija Docētājs: Dr. P. Daugulis 2008./2009.studiju
Saturs Sākums Beigas Atpakaļ Aizvērt Pilns ekrāns 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studij
 1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Veselo skaitļu teorija 7.lekcija Docētājs: Dr. P. Daugulis 2008./2009.studiju
1 DAUGAVPILS UNIVERSITĀTE Dabaszinātņu un matemātikas fakultāte Matemātikas katedra Bakalaura studiju programma Matemātika Studiju kurss Veselo skaitļu teorija 7.lekcija Docētājs: Dr. P. Daugulis 2008./2009.studiju
4
 4.pielikums Aizkraukles novada domes 2014.gada 24.janvāra saistošajiem noteikuminr.2014/1 AIZKRAUKLES NOVADA PASĀKUMU PLĀNS SPORTA NOZARĒ 2014.gadam UN NEPIECIEŠAMAIS FINANSĒJUMS Nr. p.k. Pasākums Laiks
4.pielikums Aizkraukles novada domes 2014.gada 24.janvāra saistošajiem noteikuminr.2014/1 AIZKRAUKLES NOVADA PASĀKUMU PLĀNS SPORTA NOZARĒ 2014.gadam UN NEPIECIEŠAMAIS FINANSĒJUMS Nr. p.k. Pasākums Laiks
Latvijas gada čenpionāta alpīnismā nolikums
 Latvijas Alpīnistu savienība APSTIPRINU Aiga Rakēviča LAS prezidents Rīgā, 2015. gada 26.februāri NOLIKUMS I MĒRĶIS UN UZDEVUMI 1.1.Popularizēt un veicināt kalnos kāpšanu, alpīnismu; 1.2.Noteikt labākos
Latvijas Alpīnistu savienība APSTIPRINU Aiga Rakēviča LAS prezidents Rīgā, 2015. gada 26.februāri NOLIKUMS I MĒRĶIS UN UZDEVUMI 1.1.Popularizēt un veicināt kalnos kāpšanu, alpīnismu; 1.2.Noteikt labākos
Slide 1
 transporta plūsmas monitorēšanai Roberts Kadiķis Kārlis Freivalds Multifunkcionāla inteliģenta transporta sistēmas punkta tehnoloģija Nr.2DP/2.1.1.1.0/10/APIA/VIAA/086 Motivācija Nepieciešamība efektīvāk
transporta plūsmas monitorēšanai Roberts Kadiķis Kārlis Freivalds Multifunkcionāla inteliģenta transporta sistēmas punkta tehnoloģija Nr.2DP/2.1.1.1.0/10/APIA/VIAA/086 Motivācija Nepieciešamība efektīvāk
ro41_uzd
 Materiāls ņemts no grāmatas:andžāns Agnis, Bērziņa Anna, Bērziņš Aivars "Latvijas matemātikas olimpiāžu (5-5) kārtas (rajonu) uzdevumi un atrisinājumi" LATVIJAS RAJONU 4 OLIMPIĀDE 5 klase 4 Dots, ka a
Materiāls ņemts no grāmatas:andžāns Agnis, Bērziņa Anna, Bērziņš Aivars "Latvijas matemātikas olimpiāžu (5-5) kārtas (rajonu) uzdevumi un atrisinājumi" LATVIJAS RAJONU 4 OLIMPIĀDE 5 klase 4 Dots, ka a
AGV / Apaļie gaisa vadi Izmērs AL90 / Apaļo gaisa vadu līkums 90 o Izmērs
 AGV / Apaļie gaisa vadi 100 125 160 200 250 315 355 400 450 500 560 630 710 800 900 1000 1250 AL90 / Apaļo gaisa vadu līkums 90 o 100 125 160 200 250 315 355 400 450 500 560 630 710 800 900 1000 1250 125-100
AGV / Apaļie gaisa vadi 100 125 160 200 250 315 355 400 450 500 560 630 710 800 900 1000 1250 AL90 / Apaļo gaisa vadu līkums 90 o 100 125 160 200 250 315 355 400 450 500 560 630 710 800 900 1000 1250 125-100
Rudens KampaŅa JAUDA kā instrumentiem ar vadu BRĪVĪBA kā bezvadu instrumentiem Akcijas periods:
 Rudens KampaŅa JAUDA kā instrumentiem ar vadu BRĪVĪBA kā bezvadu instrumentiem Akcijas periods: 01.08.2016. 31.10.2016. WWW.LICGOTUS.LV 18V XR XPS Leņķzāģis Akumulatoru kapacitāte 4Ah Apgriezieni min.
Rudens KampaŅa JAUDA kā instrumentiem ar vadu BRĪVĪBA kā bezvadu instrumentiem Akcijas periods: 01.08.2016. 31.10.2016. WWW.LICGOTUS.LV 18V XR XPS Leņķzāģis Akumulatoru kapacitāte 4Ah Apgriezieni min.
Microsoft PowerPoint - 2_sem_10_Rauhvargers_LO nepiec_2013.pptx
 Mācīšanās rezultātos balstītas studijas: Ko tās dod augstākajā izglītībā ieinteresētājām pusēm? Vai varam atļauties to neieviest? Prof. Andrejs Rauhvargers Kā aprakstīsim kvalifikācijas? Pateiksim, cik
Mācīšanās rezultātos balstītas studijas: Ko tās dod augstākajā izglītībā ieinteresētājām pusēm? Vai varam atļauties to neieviest? Prof. Andrejs Rauhvargers Kā aprakstīsim kvalifikācijas? Pateiksim, cik
Microsoft Word - du_5_2005.doc
 005, Pēteris Daugulis BŪLA (BINĀRĀS) FUNKCIJAS UN/VAI MATEMĀTISKĀ LOĢIKA Lietderīgi pētīt funkcijas, kuru argumenti un vērtības ir bināras virknes. Kopa {0,} tiek asociēta ar {jā, nē} vai {patiess, aplams}.
005, Pēteris Daugulis BŪLA (BINĀRĀS) FUNKCIJAS UN/VAI MATEMĀTISKĀ LOĢIKA Lietderīgi pētīt funkcijas, kuru argumenti un vērtības ir bināras virknes. Kopa {0,} tiek asociēta ar {jā, nē} vai {patiess, aplams}.
55repol_atr
 9 Pieskitot pierādāmās vienādīs L()+L()+L(3)=L(4) ām pusēm L(5)+L(6)+L(), iegūstm ekvivlentu vienādīu L()+L()=L(NM), ks cīmredzmi izriet no trijstūr un prlelogrm lukumu formulām L = h un L=h 9 ) =7, =7
9 Pieskitot pierādāmās vienādīs L()+L()+L(3)=L(4) ām pusēm L(5)+L(6)+L(), iegūstm ekvivlentu vienādīu L()+L()=L(NM), ks cīmredzmi izriet no trijstūr un prlelogrm lukumu formulām L = h un L=h 9 ) =7, =7
2012 Komandu olimpiāde Atvērtā Kopa Atrisinājumi 10. klasei 1. Tā kā LM ir viduslīnija, tad, balstoties uz viduslīnijas īpašībām, trijstūra 1 laukums
 01 Komandu olimpiāde Atvērtā Kopa Atrisinājumi 10. klasei 1. Tā kā LM ir viduslīnija, tad, balstoties uz viduslīnijas īpašībām, trijstūra 1 laukums būs 1 4 no trijstūra ABC laukuma. Analogi no viduslīnijām
01 Komandu olimpiāde Atvērtā Kopa Atrisinājumi 10. klasei 1. Tā kā LM ir viduslīnija, tad, balstoties uz viduslīnijas īpašībām, trijstūra 1 laukums būs 1 4 no trijstūra ABC laukuma. Analogi no viduslīnijām
Tirgus dal bnieka nosaukums: Ieguld jumu p rvaldes akciju sabiedr ba "Finasta Asset Management" Kods: 100 Invalda konservativais ieguldijumu plans 1.
 Tirgus dal bnieka nosaukums: p rvaldes akciju sabiedr ba "Finasta Asset Management" 1. pielikums Finanšu un kapit la tirgus komisijas 14.09.2007. noteikumiem Nr. 125 UPDK 0651293 J iesniedz Finanšu un
Tirgus dal bnieka nosaukums: p rvaldes akciju sabiedr ba "Finasta Asset Management" 1. pielikums Finanšu un kapit la tirgus komisijas 14.09.2007. noteikumiem Nr. 125 UPDK 0651293 J iesniedz Finanšu un
Prezentacija
 LATVIJAS LAUKSAIMNIECĪBAS UNIVERSITĀTE Galvenie nosacījumi reflektantu uzņemšanai pamatstudijās 2016./2017. studiju gadam UZŅEMŠANAS KOMISIJA Lielā iela 2, 180.telpa, Jelgava, LV-3001 Tālr.: 20227755,
LATVIJAS LAUKSAIMNIECĪBAS UNIVERSITĀTE Galvenie nosacījumi reflektantu uzņemšanai pamatstudijās 2016./2017. studiju gadam UZŅEMŠANAS KOMISIJA Lielā iela 2, 180.telpa, Jelgava, LV-3001 Tālr.: 20227755,
Rudens KampaŅa JAUDA kā instrumentiem ar vadu BRĪVĪBA kā bezvadu instrumentiem Akcijas periods:
 Rudens KampaŅa JAUDA kā instrumentiem ar vadu BRĪVĪBA kā bezvadu instrumentiem Akcijas periods:..6. 3..6. WWW.LICGOTUS.LV Li-Ion Kompakta akumulatoru XPS Leņķzāģis Apgriezieni min. 35rpm Ripas diametrs
Rudens KampaŅa JAUDA kā instrumentiem ar vadu BRĪVĪBA kā bezvadu instrumentiem Akcijas periods:..6. 3..6. WWW.LICGOTUS.LV Li-Ion Kompakta akumulatoru XPS Leņķzāģis Apgriezieni min. 35rpm Ripas diametrs
PowerPoint Presentation
 Šeit top veiksmīgas karjeras Galvenie nosacījumi reflektantu uzņemšanai pamatstudijās 2019./2020. studiju gadam Uzņemšanas komisija Lielā iela 2, 180.telpa, Jelgava, LV-3001 Tālr.: 20227755, e-pasts: ukom@llu.lv
Šeit top veiksmīgas karjeras Galvenie nosacījumi reflektantu uzņemšanai pamatstudijās 2019./2020. studiju gadam Uzņemšanas komisija Lielā iela 2, 180.telpa, Jelgava, LV-3001 Tālr.: 20227755, e-pasts: ukom@llu.lv
untitled
 Luonnos 190307 Stora Enso WoodPax ēvelēti kokmateriāli būvniecībai un Stora Enso WoodPax ēvelēti kokmateriāli būvniecībai un WoodPax izstrādājumu sērija piedāvā Tev uzstādīšanai gatavus ēvelētus kokmateriālus:
Luonnos 190307 Stora Enso WoodPax ēvelēti kokmateriāli būvniecībai un Stora Enso WoodPax ēvelēti kokmateriāli būvniecībai un WoodPax izstrādājumu sērija piedāvā Tev uzstādīšanai gatavus ēvelētus kokmateriālus:
DAUGAVPILS UNIVERSITĀTE Matemātikas katedra Vjačeslavs Starcevs MATEMĀTISKĀS ANALĪZES SĀKUMU ZINĀTNISKIE PAMATI (izvēles tēmas) 2008
 DAUGAVPILS UNIVERSITĀTE Matemātikas katedra Vjačeslavs Starcevs MATEMĀTISKĀS ANALĪZES SĀKUMU ZINĀTNISKIE PAMATI (izvēles tēmas) 2008 ANOTĀCIJA Piedāvātie materiāli (izvēles tēmas) ir paredzēti matemātikas
DAUGAVPILS UNIVERSITĀTE Matemātikas katedra Vjačeslavs Starcevs MATEMĀTISKĀS ANALĪZES SĀKUMU ZINĀTNISKIE PAMATI (izvēles tēmas) 2008 ANOTĀCIJA Piedāvātie materiāli (izvēles tēmas) ir paredzēti matemātikas
Studiju programmas nosaukums
 Latvijas augstāko izglītības iestāžu ieguldījums mērniecības izglītībā Latvijā Jauno jomas speciālistu sagatavošana Latvijas Lauksaimniecības specialitātē Vivita Puķīte LLU VBF Zemes pārvaldības un ģeodēzijas
Latvijas augstāko izglītības iestāžu ieguldījums mērniecības izglītībā Latvijā Jauno jomas speciālistu sagatavošana Latvijas Lauksaimniecības specialitātē Vivita Puķīte LLU VBF Zemes pārvaldības un ģeodēzijas
A.Broks Studiju kursa DOMĀŠANAS SISTEMOLOĢIJA nodarbību shematiskie konspekti DS - PRIEKŠVĀRDS
 DS - PRIEKŠVĀRDS 2012-13 1 DS - PRIEKŠVĀRDS 2012-13 2 DS - PRIEKŠVĀRDS 2012-13 3 Komentāri par studiju kursa b ū t ī b u un s ū t ī b u Būtība veicot sistēmiskās domāšanas kā domāšanas sistēmiskuma apzināšanu,
DS - PRIEKŠVĀRDS 2012-13 1 DS - PRIEKŠVĀRDS 2012-13 2 DS - PRIEKŠVĀRDS 2012-13 3 Komentāri par studiju kursa b ū t ī b u un s ū t ī b u Būtība veicot sistēmiskās domāšanas kā domāšanas sistēmiskuma apzināšanu,
Microsoft Word - SEG_ atskaite_Bolderaja_2008.doc
 SIA Bolderaja Ltd Pārskats par siltumnīcefekta gāzu emisiju 2008.gadā. Saturs I. Ziņas par operatoru.. 3 II. Vispārīga informācija par piesārņojošām darbībām. 4 III. Emisijas aprēķini sadedzināšanas procesiem
SIA Bolderaja Ltd Pārskats par siltumnīcefekta gāzu emisiju 2008.gadā. Saturs I. Ziņas par operatoru.. 3 II. Vispārīga informācija par piesārņojošām darbībām. 4 III. Emisijas aprēķini sadedzināšanas procesiem
VALDES ZIŅOJUMS PAR LSA DARBĪBU 2018./2019. GADĀ Ziņo: prezidente J.Širina
 VALDES ZIŅOJUMS PAR LSA DARBĪBU 2018./2019. GADĀ Ziņo: prezidente J.Širina Par spīti organizācijas darbības iekšējiem izaicinājumiem pārskata periodā, LSA aktualizējusi un risinājusi virkni problēmjautājumu,
VALDES ZIŅOJUMS PAR LSA DARBĪBU 2018./2019. GADĀ Ziņo: prezidente J.Širina Par spīti organizācijas darbības iekšējiem izaicinājumiem pārskata periodā, LSA aktualizējusi un risinājusi virkni problēmjautājumu,
Ēkas energosertifikāts REĢISTRĀCIJAS NUMURS a311 DERĪGS LĪDZ - 1. Ēkas veids daudzdzīvokļu māja 2.1 Adrese Kokneses nov., Kokneses p
 Ēkas energosertifikāts REĢISTRĀCIJAS NUMURS 017018-19-7a311 DERĪGS LĪDZ - 1. Ēkas veids daudzdzīvokļu māja.1 Adrese Kokneses nov., Kokneses pag., Koknese, Indrānu iela 3.1 Ēkas daļa -.1 Ēkas vai tās daļas
Ēkas energosertifikāts REĢISTRĀCIJAS NUMURS 017018-19-7a311 DERĪGS LĪDZ - 1. Ēkas veids daudzdzīvokļu māja.1 Adrese Kokneses nov., Kokneses pag., Koknese, Indrānu iela 3.1 Ēkas daļa -.1 Ēkas vai tās daļas
Rīgas Tehniskā universitāte. Inženiermatemātikas katedra. Lekciju konspekts. Kompleksā mainīgā funkciju teorijas nozīme Kompleksā mainīgā funkciju teo
 Kompleksā mainīgā funkciju teoijas noīme Kompleksā mainīgā funkciju teoija adās 8 gadsimtā, un tās pamatlicēji i fanču matemātiķis Žans Leons Dalambēs un šveiciešu matemātiķis Leonads Eiles Daud ieguldījumu
Kompleksā mainīgā funkciju teoijas noīme Kompleksā mainīgā funkciju teoija adās 8 gadsimtā, un tās pamatlicēji i fanču matemātiķis Žans Leons Dalambēs un šveiciešu matemātiķis Leonads Eiles Daud ieguldījumu
Sarakstā apkopotas adreses ēkām, kurām ir valsts vai vietējās nozīmes kultūras pieminekļa statuss OBJECTID ADRESE BNOS KAD. APZĪMĒJUMS 1 Alejas iela 1
 Sarakstā apkopotas adreses ēkām, kurām ir valsts vai vietējās nozīmes kultūras pieminekļa statuss OBJECTID ADRESE BNOS KAD. APZĪMĒJUMS 1 Alejas iela 10 Dzīvojamā ēka 17000360256001 2 Alejas iela 11 Dzīvojamā
Sarakstā apkopotas adreses ēkām, kurām ir valsts vai vietējās nozīmes kultūras pieminekļa statuss OBJECTID ADRESE BNOS KAD. APZĪMĒJUMS 1 Alejas iela 10 Dzīvojamā ēka 17000360256001 2 Alejas iela 11 Dzīvojamā
1
 . Ļ Uzdevumos. 5. apvelc pareizai atbildei atbilstošo burtu. 75 minūtes ir: 0.75 h.5 h. h.5 h. Sešstūra piramīdas skaldņu skaits ir: 6 7 8. Izteiksmes log vērtība ir: -. Nevienādības x 0atrisinājums ir
. Ļ Uzdevumos. 5. apvelc pareizai atbildei atbilstošo burtu. 75 minūtes ir: 0.75 h.5 h. h.5 h. Sešstūra piramīdas skaldņu skaits ir: 6 7 8. Izteiksmes log vērtība ir: -. Nevienādības x 0atrisinājums ir
Microsoft Word - Vēlēšanu nolikums projekts.docx
 Latvijas Universitātes Studentu padome Reģ. Nr.40008009084 Raiņa bulvāris 19-144, LV-1586, Rīga, Latvija Tālrunis 67034317, Fakss 67034316, E-pasts: lusp@lusp.lv APSTIPRINĀTS LU Studentu padomes 2006.gada
Latvijas Universitātes Studentu padome Reģ. Nr.40008009084 Raiņa bulvāris 19-144, LV-1586, Rīga, Latvija Tālrunis 67034317, Fakss 67034316, E-pasts: lusp@lusp.lv APSTIPRINĀTS LU Studentu padomes 2006.gada
TIRGUS IZPĒTE Mobilo sakaru pakalpojumi Informācija par Pasūtītāju: Nosaukums Kurzemes plānošanas reģions Reģistrācijas numurs Juridiskā a
 TIRGUS IZPĒTE Mobilo sakaru pakalpojumi Informācija par Pasūtītāju: Nosaukums Kurzemes plānošanas reģions Reģistrācijas numurs 90002183562 Juridiskā adrese Avotu iela 12, Saldus, Saldus novads, LV-3801
TIRGUS IZPĒTE Mobilo sakaru pakalpojumi Informācija par Pasūtītāju: Nosaukums Kurzemes plānošanas reģions Reģistrācijas numurs 90002183562 Juridiskā adrese Avotu iela 12, Saldus, Saldus novads, LV-3801
[Type here] Būvniecības ieceres 2017.gadā. Paskaidrojuma raksti, apliecinājuma kartes, tehniskās shēmas Nr. p.p. Iesnieguma datums Lietas Nr
![[Type here] Būvniecības ieceres 2017.gadā. Paskaidrojuma raksti, apliecinājuma kartes, tehniskās shēmas Nr. p.p. Iesnieguma datums Lietas Nr [Type here] Būvniecības ieceres 2017.gadā. Paskaidrojuma raksti, apliecinājuma kartes, tehniskās shēmas Nr. p.p. Iesnieguma datums Lietas Nr](/thumbs/88/116296898.jpg) Būvniecības ieceres 2017.gadā. Paskaidrojuma raksti, apliecinājuma kartes, tehniskās shēmas Nr. p.p. esnieguma datums Lietas Nr. 1. 03.01.2017. 3.5.10/01-PR2017 BS-23664-173 2. 06.01.2017. 3.5.10/02-PR2017
Būvniecības ieceres 2017.gadā. Paskaidrojuma raksti, apliecinājuma kartes, tehniskās shēmas Nr. p.p. esnieguma datums Lietas Nr. 1. 03.01.2017. 3.5.10/01-PR2017 BS-23664-173 2. 06.01.2017. 3.5.10/02-PR2017
1. Oskars Valtenbergs - Pozitīvais sponsoru līderis Studiju programma, kurss: Ķīmijas maģistrs, 2.kurss KANDIDĒJU ĶF SP, JO ar savu uzkrāto pieredzi v
 1. Oskars Valtenbergs - Pozitīvais sponsoru līderis Studiju programma, kurss: Ķīmijas maģistrs, 2.kurss KANDIDĒJU ĶF SP, JO ar savu uzkrāto pieredzi vēlos turpināt uzlabot ĶF SP darbību, kā arī nest ķīmiķu
1. Oskars Valtenbergs - Pozitīvais sponsoru līderis Studiju programma, kurss: Ķīmijas maģistrs, 2.kurss KANDIDĒJU ĶF SP, JO ar savu uzkrāto pieredzi vēlos turpināt uzlabot ĶF SP darbību, kā arī nest ķīmiķu
PowerPoint Presentation
 Liene Kubliņa liene.kublina@cvor.lv www.cvor.lv IT nozares attīstības iespējas ierobežota darba tirgus apstākļos Latvijas darba tirgus Ko dara Latvijas IT uzņēmumi Patiesie motivatori un jēgpilna komandas
Liene Kubliņa liene.kublina@cvor.lv www.cvor.lv IT nozares attīstības iespējas ierobežota darba tirgus apstākļos Latvijas darba tirgus Ko dara Latvijas IT uzņēmumi Patiesie motivatori un jēgpilna komandas
Rīgā gada. jūnijā 1. PAPILDU VIENOŠANĀS Nr. LB-07/2017/ gada 2. maija līgumam Nr. LB-07/2017/177 Par būvdarbiem, grīdas konstrukcijas u
 Rīgā 2017. gada. jūnijā 1. PAPILDU VIENOŠANĀS Nr. LB-07/2017/269 2017. gada 2. maija līgumam Nr. LB-07/2017/177 Par būvdarbiem, grīdas konstrukcijas un seguma nomaiņu un starpsienas skaņas izolācijas uzlabošanu,
Rīgā 2017. gada. jūnijā 1. PAPILDU VIENOŠANĀS Nr. LB-07/2017/269 2017. gada 2. maija līgumam Nr. LB-07/2017/177 Par būvdarbiem, grīdas konstrukcijas un seguma nomaiņu un starpsienas skaņas izolācijas uzlabošanu,
48repol_uzd
 Materiāls ņemts o grāmatas: Adžās Agis, Bērziņa Aa, Bērziņš Aivars "Latvijas Republikas 6.-5. matemātikas olimpiādes" LATVIJAS REPUBLIKAS 48. OLIMPIĀDE UZDEVUMI 9. klase 48.. Ziāms, ka 48..zīm. attēlots
Materiāls ņemts o grāmatas: Adžās Agis, Bērziņa Aa, Bērziņš Aivars "Latvijas Republikas 6.-5. matemātikas olimpiādes" LATVIJAS REPUBLIKAS 48. OLIMPIĀDE UZDEVUMI 9. klase 48.. Ziāms, ka 48..zīm. attēlots
Intra_2019_16iter_lv_embed_280519
 Kompleksu gāzes sistēmu risinājumi Ražošana/Montāža/Pārdošana 2019 Komandas pieredze Pieredzes un azarta sinerģija kopš 1994. gada Padomju gāzes staciju modernizācijas eksperti Vairums darbinieku strādā
Kompleksu gāzes sistēmu risinājumi Ražošana/Montāža/Pārdošana 2019 Komandas pieredze Pieredzes un azarta sinerģija kopš 1994. gada Padomju gāzes staciju modernizācijas eksperti Vairums darbinieku strādā
Latvijas Universitātes Studentu padome Reģ. Nr Raiņa bulvāris , LV-1586, Rīga, Latvija Tālrunis , Fakss , E-pasts: l
 Latvijas Universitātes Studentu padome Reģ. Nr.40008009084 Raiņa bulvāris 19-144, LV-1586, Rīga, Latvija Tālrunis 67034317, Fakss 67034316, E-pasts: lusp@lusp.lv APSTIPRINĀTS 22.02.2010. Latvijas Universitātes
Latvijas Universitātes Studentu padome Reģ. Nr.40008009084 Raiņa bulvāris 19-144, LV-1586, Rīga, Latvija Tālrunis 67034317, Fakss 67034316, E-pasts: lusp@lusp.lv APSTIPRINĀTS 22.02.2010. Latvijas Universitātes
Pamatelementi statistikā un Hipotēžu pārbaude
 Pamatelementi statistikā un Hipotēžu pārbaude J. Valeinis 1 1 Latvijas Universitāte, Rīga 12.marts, 2010 Valeinis Pamatelementi statistikā un Hipotēžu pārbaude p. 1 of 22 Ievads I. Pamatelementi matemātiskajā
Pamatelementi statistikā un Hipotēžu pārbaude J. Valeinis 1 1 Latvijas Universitāte, Rīga 12.marts, 2010 Valeinis Pamatelementi statistikā un Hipotēžu pārbaude p. 1 of 22 Ievads I. Pamatelementi matemātiskajā
1
 8. Datu struktūras un aritmētika Nodaļas saturs 8. Datu struktūras un aritmētika...8-1 8.1. Vienkāršie datu objekti...8-1 8.2. Datu apviešana struktūrās, izmantojot funktorus...8-1 8.3. Terma jēdziena
8. Datu struktūras un aritmētika Nodaļas saturs 8. Datu struktūras un aritmētika...8-1 8.1. Vienkāršie datu objekti...8-1 8.2. Datu apviešana struktūrās, izmantojot funktorus...8-1 8.3. Terma jēdziena
06LV0061
 Kabeļu kanāli darbam un mājai Grīdlīstes kanāli perfekta elektroinstalācija Papildus info mūsu mājas lapā Modernas elektroinstalācijas ierīkošana bieži vien saistīta ar lieliem ieguldījumiem. Vadu un kabeļu
Kabeļu kanāli darbam un mājai Grīdlīstes kanāli perfekta elektroinstalācija Papildus info mūsu mājas lapā Modernas elektroinstalācijas ierīkošana bieži vien saistīta ar lieliem ieguldījumiem. Vadu un kabeļu
AS "Latvenergo" saimnieciskajā darbībā neizmantojamo transportlīdzekļu saraksts un sākuma cenas izsolei Stopiņu novada Līčos, Rīgas ielā 14
 tips Valsts reģ. Izlaiduma gads eksperta 1 LLT, 8101 Piekabe kravas kaste A5496 1997 3 (viduvējs) 50.00 06.61 apskates ZIL, 130 Kravas kaste AV6133 1987 84307 3 (viduvējs) 400.00 330.58 LIEPĀJA, CUKURA
tips Valsts reģ. Izlaiduma gads eksperta 1 LLT, 8101 Piekabe kravas kaste A5496 1997 3 (viduvējs) 50.00 06.61 apskates ZIL, 130 Kravas kaste AV6133 1987 84307 3 (viduvējs) 400.00 330.58 LIEPĀJA, CUKURA
SANCO/11120/2012-EN
 EIROPAS SAVIENĪBAS PADOME Briselē, 2012. gada 26. septembrī (27.09) (OR. en) 14269/12 DENLEG 93 AGRI 626 PAVADVĒSTULE Sūtītājs: Eiropas Komisija Saņemšanas datums: 2012. gada 18. septembris Saņēmējs: Padomes
EIROPAS SAVIENĪBAS PADOME Briselē, 2012. gada 26. septembrī (27.09) (OR. en) 14269/12 DENLEG 93 AGRI 626 PAVADVĒSTULE Sūtītājs: Eiropas Komisija Saņemšanas datums: 2012. gada 18. septembris Saņēmējs: Padomes
1 Pielikums Rīgas domes lēmumam Nr.5376 Līdzfinansējuma apmērs interešu izglītības un pieaugušo neformālās izglītības programmām Rīgas pil
 1 Pielikums Rīgas domes 23.10.2012. lēmumam Nr.5376 interešu izglītības un pieaugušo neformālās izglītības programmām Rīgas pilsētas pašvaldības izglītības iestādēs un tā aprēķināšanas kārtība 1. 1.1.
1 Pielikums Rīgas domes 23.10.2012. lēmumam Nr.5376 interešu izglītības un pieaugušo neformālās izglītības programmām Rīgas pilsētas pašvaldības izglītības iestādēs un tā aprēķināšanas kārtība 1. 1.1.
Pārskats par Latvijas valsts simtgades pasākumu plāna – 2021.gadam īstenošanai piešķirtā valsts budžeta finansējuma izlietojumu 20___. gadā
 Pielikums Ministru kabineta 2016. gada 13. decembra rīkojumam Nr. 769 Pārskats par Latvijas valsts simtgades pasākumu plāna 2017. 2021. gadam īstenošanai piešķirtā valsts budžeta finansējuma izlietojumu
Pielikums Ministru kabineta 2016. gada 13. decembra rīkojumam Nr. 769 Pārskats par Latvijas valsts simtgades pasākumu plāna 2017. 2021. gadam īstenošanai piešķirtā valsts budžeta finansējuma izlietojumu
Jaunais Crafter Modelis Dzinējs Jauda Transmisija Pilnā masa Kravnesība Cena Kods Tips kw / Zs Tips kg EUR ar PVN Crafter 30 Kasten
 Jaunais Crafter Modelis Dzinējs Jauda Transmisija Pilnā masa Kravnesība Tips kw / Zs Tips kg Crafter 30 Kasten standarta garenbāze SYBA2A 2.0 TDI 75/ 102 6G priekšpiedziņa 3,000 978-384 24 869 SYBA4Y 2.0
Jaunais Crafter Modelis Dzinējs Jauda Transmisija Pilnā masa Kravnesība Tips kw / Zs Tips kg Crafter 30 Kasten standarta garenbāze SYBA2A 2.0 TDI 75/ 102 6G priekšpiedziņa 3,000 978-384 24 869 SYBA4Y 2.0
PowerPoint Presentation
 2018./2019.m.g. rezultāti un prioritātes 2019./2020.m.g. Daugavpils pilsētas Izglītības pārvaldes vadītāja Marina Isupova 09.07.2019. Mācību gada noslēgums vispārizglītojošo skolu 12.kl.absolventiem Ministru
2018./2019.m.g. rezultāti un prioritātes 2019./2020.m.g. Daugavpils pilsētas Izglītības pārvaldes vadītāja Marina Isupova 09.07.2019. Mācību gada noslēgums vispārizglītojošo skolu 12.kl.absolventiem Ministru
S-7-1, , 7. versija Lappuse 1 no 5 KURSA KODS STUDIJU KURSA PROGRAMMAS STRUKTŪRA Kursa nosaukums latviski Varbūtību teorija un matemātiskā
 Lappuse 1 no 5 KURSA KODS STUDIJU KURSA PROGRAMMAS STRUKTŪRA Kursa nosaukums latviski Varbūtību teorija un matemātiskā statistika I, II Kursa nosaukums angliski A Theory of Probability and Mathematical
Lappuse 1 no 5 KURSA KODS STUDIJU KURSA PROGRAMMAS STRUKTŪRA Kursa nosaukums latviski Varbūtību teorija un matemātiskā statistika I, II Kursa nosaukums angliski A Theory of Probability and Mathematical
Sociālo tīklu neizmērojamais spēks
 Sociālo tīklu neizmērojamais spēks Sociālo tīklu izplatība Latvijā lieto 2/3 Latvijas iedzīvotāju Populārākie Draugiem (1.2M/ 665 tk), Facebook (415 tk), Youtube un Twitter (180 tk/ 82 tk) Facebook & Draugiem.lv
Sociālo tīklu neizmērojamais spēks Sociālo tīklu izplatība Latvijā lieto 2/3 Latvijas iedzīvotāju Populārākie Draugiem (1.2M/ 665 tk), Facebook (415 tk), Youtube un Twitter (180 tk/ 82 tk) Facebook & Draugiem.lv
Microsoft Word - Noteikumi_Dizaina pakalpojumi_
 VAS STARPTAUTISKĀ LIDOSTA RĪGA Tirgus izpētes Dizaina pakalpojumu sniegšana VAS Starptautiskā lidosta Rīgā (Identifikācijas Nr. TI-13/60) NOTEIKUMI M rupes novad 1. VISPĀRĪGĀ INFORMĀCIJA 1.1. Pasūtītājs
VAS STARPTAUTISKĀ LIDOSTA RĪGA Tirgus izpētes Dizaina pakalpojumu sniegšana VAS Starptautiskā lidosta Rīgā (Identifikācijas Nr. TI-13/60) NOTEIKUMI M rupes novad 1. VISPĀRĪGĀ INFORMĀCIJA 1.1. Pasūtītājs
 Page 1 of 8 Biedrību, nodibinājumu un arodbiedrību gada pārskats: Bilance - Aktīvs Taksācijas periods no: 01.01.2009 līdz: 31.12.2009 Bilance - Aktīvs Bilancē summas jānorāda veselos latos. Nr. p.k. Posteņa
Page 1 of 8 Biedrību, nodibinājumu un arodbiedrību gada pārskats: Bilance - Aktīvs Taksācijas periods no: 01.01.2009 līdz: 31.12.2009 Bilance - Aktīvs Bilancē summas jānorāda veselos latos. Nr. p.k. Posteņa
2. pielikums Rīgas Stradiņa universitātes Kvalitātes rokasgrāmatai Aktualizēta gada 26. jūnija Senāta sēdē, protokols Nr. 2-1/ RĪGAS STR
 2. pielikums Rīgas Stradiņa universitātes Kvalitātes rokasgrāmatai RĪGAS STRADIŅA UNIVERSITĀTES PAKĻAUTĪBU STRUKTŪRSHĒMA Satversmes sapulce Akadēmiskā šķirējtiesa Senāts Rektors* Studējošo pašpārvalde
2. pielikums Rīgas Stradiņa universitātes Kvalitātes rokasgrāmatai RĪGAS STRADIŅA UNIVERSITĀTES PAKĻAUTĪBU STRUKTŪRSHĒMA Satversmes sapulce Akadēmiskā šķirējtiesa Senāts Rektors* Studējošo pašpārvalde
COMBO LIFE
 COMBO LIFE Opel COMBO LIFE Combo Life Pārnesumkārba kw ZS CO 2 izmeši (g/km) WLTP L1H1 L1H1 L2H1 1.2 Turbo ECOTEC Start/Stop 0DL26 EH61 / XIAA M6 81 110 157 1.5 DT ECOTEC Start/Stop 0DL26 HE51 / XIAA M5
COMBO LIFE Opel COMBO LIFE Combo Life Pārnesumkārba kw ZS CO 2 izmeši (g/km) WLTP L1H1 L1H1 L2H1 1.2 Turbo ECOTEC Start/Stop 0DL26 EH61 / XIAA M6 81 110 157 1.5 DT ECOTEC Start/Stop 0DL26 HE51 / XIAA M5
PowerPoint Presentation
 2018. 2019. gada kampaņa «Turi grožos bīstamās vielas» Renārs Lūsis Valsts darba inspekcijas direktors Kas ir bīstamas vielas? Jebkura viela (gāze, šķidrums vai cieta viela), kas apdraud darbinieku drošību
2018. 2019. gada kampaņa «Turi grožos bīstamās vielas» Renārs Lūsis Valsts darba inspekcijas direktors Kas ir bīstamas vielas? Jebkura viela (gāze, šķidrums vai cieta viela), kas apdraud darbinieku drošību
Publiskā apspriešana
 BŪVNIECĪBS IECERES PUBLISKĀ PSPRIEŠN JUNS TRMVJU INFRSTRUKTŪRS POSM IZBŪVE UN ESOŠS TRMVJU LĪNIJS PĀRBŪVE. BŪVNIECĪBS IEROSINĀTĀJS: Rīgas Pašvaldības SI Rīgas satiksme Reģ.Nr.40003619950, Kleistu 28, Rīga,
BŪVNIECĪBS IECERES PUBLISKĀ PSPRIEŠN JUNS TRMVJU INFRSTRUKTŪRS POSM IZBŪVE UN ESOŠS TRMVJU LĪNIJS PĀRBŪVE. BŪVNIECĪBS IEROSINĀTĀJS: Rīgas Pašvaldības SI Rīgas satiksme Reģ.Nr.40003619950, Kleistu 28, Rīga,
7. Tēma: Polinomi ar veseliem koeficientiem Uzdevums 7.1 (IMO1982.4): Prove that if n is a positive integer such that the equation x 3 3xy 2 + y 3 = n
 7. Tēma: Polinomi ar veseliem koeficientiem Uzdevums 7.1 (IMO1982.): Prove that if n is a positive integer such that the equation x xy 2 + y = n has a solution in integers x, y, then it has at least three
7. Tēma: Polinomi ar veseliem koeficientiem Uzdevums 7.1 (IMO1982.): Prove that if n is a positive integer such that the equation x xy 2 + y = n has a solution in integers x, y, then it has at least three
Kablolar ve Adaptörler Ürün Marka Stok Fiyat INCA IPW-15TP POWER KABLO 1,5 METRE Inca 10+ 2,10 USD INCA IPR-01 USB 2.0 YAZICI KABLOSU+ASKILI (1.5MT) I
 Kablolar ve Adaptörler Ürün Marka Stok Fiyat INCA IPW-15TP POWER KABLO 1,5 METRE Inca 10+ 2,10 USD INCA IPR-01 USB 2.0 YAZICI KABLOSU+ASKILI (1.5MT) Inca 10+ 3,15 USD INCA IMHD-15T HDMI KABLO 1,8 METRE
Kablolar ve Adaptörler Ürün Marka Stok Fiyat INCA IPW-15TP POWER KABLO 1,5 METRE Inca 10+ 2,10 USD INCA IPR-01 USB 2.0 YAZICI KABLOSU+ASKILI (1.5MT) Inca 10+ 3,15 USD INCA IMHD-15T HDMI KABLO 1,8 METRE
Microsoft Word - 240_NOT_IPP_SAGAT
 Spēkā no 4.11.011. Publicēts laikrakstā Latvijas Vēstnesis Nr. 184 3.11.011. 011. gada 11. novembrī Normatīvie noteikumi Nr. 40 Rīgā (Finanšu un kapitāla tirgus komisijas padomes sēdes protokols Nr. 43.
Spēkā no 4.11.011. Publicēts laikrakstā Latvijas Vēstnesis Nr. 184 3.11.011. 011. gada 11. novembrī Normatīvie noteikumi Nr. 40 Rīgā (Finanšu un kapitāla tirgus komisijas padomes sēdes protokols Nr. 43.
Kablolar ve Adaptörler Ürün Marka Stok Fiyat INCA IMHD-15T HDMI KABLO 1,8 METRE Inca 1 3,15 USD DIGITUS USB UZATMA KABLOSU 1.8MT(AK S) Digi
 Kablolar ve Adaptörler Ürün Marka Stok Fiyat INCA IMHD-15T HDMI KABLO 1,8 METRE Inca 1 3,15 USD DIGITUS USB UZATMA KABLOSU 1.8MT(AK-300200-018-S) Digitus 3 3,68 USD INCA INPW-06TP NOTEBOOK POWER KABLO
Kablolar ve Adaptörler Ürün Marka Stok Fiyat INCA IMHD-15T HDMI KABLO 1,8 METRE Inca 1 3,15 USD DIGITUS USB UZATMA KABLOSU 1.8MT(AK-300200-018-S) Digitus 3 3,68 USD INCA INPW-06TP NOTEBOOK POWER KABLO
P7_Marko_KEA
 Pētniecības projekta nr. P7 «Jaunāko līmēšanas un aizsargājoši dekoratīvās apstrādes tehnoloģiju validācija augstas pievienotās vērtības koksnes produktu ražošanai» 3.Starpposma rezultāta atskaite SIA
Pētniecības projekta nr. P7 «Jaunāko līmēšanas un aizsargājoši dekoratīvās apstrādes tehnoloģiju validācija augstas pievienotās vērtības koksnes produktu ražošanai» 3.Starpposma rezultāta atskaite SIA
1
 . ndžāns, L. Rmān,. Johnnessons VEKTORI. DĻ y X M M O N X N x K Rīg 006 UDK. ndžāns, L. Rmān,. Johnnessons. Vektori.. dļ. Rīg: Ltvijs Universitātes kdēmiskis pgāds, 006. 7 lpp. Šjā drbā plūkoti pmtjutājumi,
. ndžāns, L. Rmān,. Johnnessons VEKTORI. DĻ y X M M O N X N x K Rīg 006 UDK. ndžāns, L. Rmān,. Johnnessons. Vektori.. dļ. Rīg: Ltvijs Universitātes kdēmiskis pgāds, 006. 7 lpp. Šjā drbā plūkoti pmtjutājumi,
Autors: Dace Copeland Andras Otto ilustrācijas Gaŗā gultā gailis guļ. Gaiļa gultā graudu grēdas. Gailis graudu grēdas ēd. Kā var gailis gultā gulēt? V
 Autors: Dace Copeland Andras Otto ilustrācijas Gaŗā gultā gailis guļ. Gaiļa gultā graudu grēdas. Gailis graudu grēdas ēd. Kā var gailis gultā gulēt? Vai tad galu galā graudu grēdas gailim nespiež galvu?
Autors: Dace Copeland Andras Otto ilustrācijas Gaŗā gultā gailis guļ. Gaiļa gultā graudu grēdas. Gailis graudu grēdas ēd. Kā var gailis gultā gulēt? Vai tad galu galā graudu grēdas gailim nespiež galvu?
IEGULDĪJUMS TAVĀ NĀKOTNĒ Projekts Nr. 2009/0216/1DP/ /09/APIA/VIAA/044 NESTRIKTAS KOPAS AR VĒRTĪBĀM PUSGREDZENĀ UN MONĀDES PĀR KATEGORIJU Jāni
 IEGULDĪJUMS TAVĀ NĀKOTNĒ Projekts Nr. 2009/0216/1DP/1.1.1.2.0/09/APIA/VIAA/044 NESTRIKTAS KOPAS AR VĒRTĪBĀM PUSGREDZENĀ UN MONĀDES PĀR KATEGORIJU Jānis Cīrulis Latvijas Universitāte email: jc@lanet.lv
IEGULDĪJUMS TAVĀ NĀKOTNĒ Projekts Nr. 2009/0216/1DP/1.1.1.2.0/09/APIA/VIAA/044 NESTRIKTAS KOPAS AR VĒRTĪBĀM PUSGREDZENĀ UN MONĀDES PĀR KATEGORIJU Jānis Cīrulis Latvijas Universitāte email: jc@lanet.lv
Nakts_labirints.xlsx
 IZAICINĀJUMS 1 GR3186 Normunds Laipnieks Suzuki Jimny 16:46 23:27:28 06:41 0 16:56:18 00:10:18 618 5 45 20 2645 1 2 PT98 Uldis Moisejs MITSUBISHI PAJERO 16:32 23:15:22 06:43 0 16:42:09 00:10:09 609 4 41
IZAICINĀJUMS 1 GR3186 Normunds Laipnieks Suzuki Jimny 16:46 23:27:28 06:41 0 16:56:18 00:10:18 618 5 45 20 2645 1 2 PT98 Uldis Moisejs MITSUBISHI PAJERO 16:32 23:15:22 06:43 0 16:42:09 00:10:09 609 4 41
PowerPoint Presentation
 Eiropas Savienības programma JAUNATNE DARBĪBĀ 2007.gada 01.janvāris 2013.gada 31.decembris v/a Jaunatnes starptautisko programmu aģentūra jauniešu neformālā izglītība JSPA darbības virzieni ES programma
Eiropas Savienības programma JAUNATNE DARBĪBĀ 2007.gada 01.janvāris 2013.gada 31.decembris v/a Jaunatnes starptautisko programmu aģentūra jauniešu neformālā izglītība JSPA darbības virzieni ES programma
EPL_elementi
 Elektropārvades līniju elementu katalogs Traversas, kāši, kronšteini un citi elementi elektropārvades līnijām Saturs Ievads... 1. Āķi...4 2. Balstu savilces un atgāžņu mezgli...7. Traversas...9 4. Tapas...18
Elektropārvades līniju elementu katalogs Traversas, kāši, kronšteini un citi elementi elektropārvades līnijām Saturs Ievads... 1. Āķi...4 2. Balstu savilces un atgāžņu mezgli...7. Traversas...9 4. Tapas...18
